The other day I mentioned how if you arrange spheres into a pyramid of hexagons, you get the same number of spheres as if you’d arranged them into a cube. Today I thought it might be nice to prove it.
Well, supposed we have just one sphere. We can think of this either as the tip of a pyramid or as a 1×1×1 cube. What we need to show is that every time we add a layer of hexagons to the base of the pyramid (to make a bigger pyramid), we get the same number of spheres as if we’d arranged the spheres into a cube.
So first, let’s ask how many more spheres there are in the N3 arrangement below right than in the (N-1)3 arrangement below left:
 |
 |
|---|
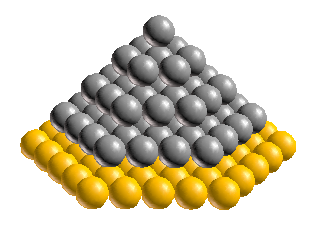
What we need to show is that this difference is the same as the number of extra spheres needed to add an Nth layer to a pyramid of hexagons. In the image below, the new layer is highlighted in gold:
Going back to the cubes, let’s color all of those extra spheres in the N3 cube:
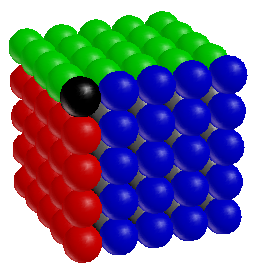
Notice that we get three extra walls — each with N×(N-1) spheres — plus one extra sphere in the corner. But that’s exactly how many spheres we need to make a hexagon with N spheres on each side:
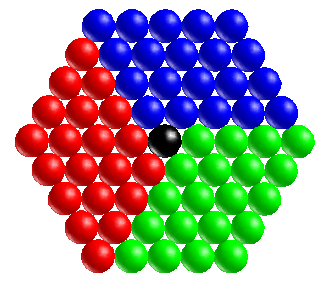
So there you have it. We just showed that each additional hexagon layer contains exactly the difference between an (N-1)3 cube and and an N3 cube. So now we can be sure that a pyramid of hexagons, stacked N high, will always add up to exactly N3 spheres!
Dear Ken,
I enjoyed reading this page. Very simple and easy to understand. I have figured out a new way to stack spheres in a hexagonal way with 2 different layers. Perhaps it may interest you.
https://m.youtube.com/watch?v=pFnDw9FRVpQ
Respectfully
Mark Slater
Very cool technique!!