Let’s say our two dimensional creature is named Ariel (which sounds like “area”) and our one dimensional being is named “Lenny” (which sounds like “length”).
Let’s also assume that Lenny can detect color as well as something equivalent to what we might call “thickness” — which might appear to him as a more vivid color, or some sort of texture, or perhaps a greater visual density.
When Ariel wants to show various shapes to Lenny, she can use both thickness and color to suggest a second dimension.
For example, suppose Ariel wants to convey the idea of “a square” or “a diamond”. To us these are rotated versions of the same shape, but to Lenny, rotation is a very advanced concept indeed, so Ariel will present them as different shapes.
Lenny can see only an “x” dimension, but Ariel asks him to imagine an extra “y” dimension. Ariel uses both “redder” and “thicker” to convey “nearer in y”, and “bluer” and “thinner” to convey “further away in y”. Of course to Lenny these are just abstractions — but Lenny understands them because he already has experience with “near” and “far” along his own x dimension.
Below are a square (top) and a diamond (bottom). In each case, on the left is what Ariel sees, and on the right is what she draws for Lenny (the gray arrows show Ariel’s idea of the correct viewing direction for each shape):
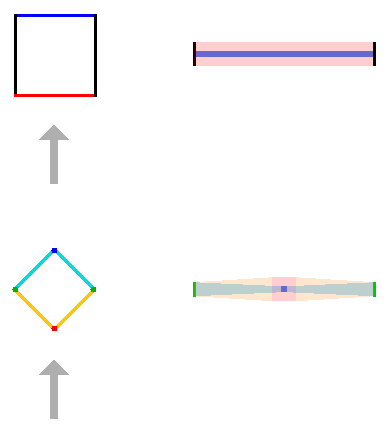
Lenny discovers that he can use his powers of imagination to understand these two shapes, which makes him feel rather clever.
But then Ariel tells Lenny that the square and diamond are actually the same shape — each is just a rotated view of the other.
As you might imagine, Lenny finds this very challenging. After all, he has no experience at all with the concept of rotation. “Oh dear,” he tells her, “I’m afraid this is going to require some non-linear thinking.”