In order to understand what’s going on with a 4D virtual trackball, let’s take a more careful look at a 3D virtual trackball.
What you see is something like this:
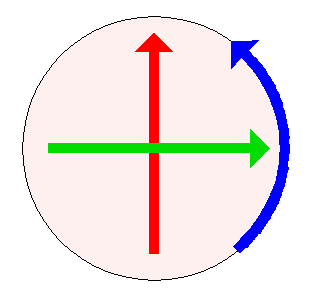
You can move your finger up and down (ie: in the direction of the red arrow), or from side to side (ie: in the direction of the green arrow), or around the circle (ie: in the direction of the blue arrow).
In each case, you are causing a sphere to rotate. This might seem mysterious to a denizen of Flatland, who does not have any direct perception of a third dimension. After all, the first two gestures look like straight line movement — very different from the circular movement of the third gesture.
Fortunately we are, in fact, 3D creatures. Which means we can employ a great 3D power-up to see what’s going on: We can rotate our view of the object:
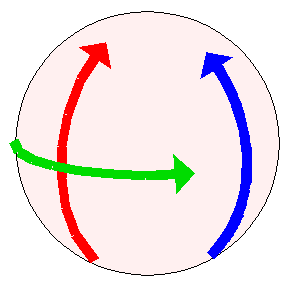
Now we can see, viewing from an oblique angle, that all three of the movements are actually circular arcs. The only reason the red and green gestures look straight is that the user cannot directly perceive the third dimension, since the z direction is perpendicular to our view. The red and green paths actually curve toward us, around the front of the sphere.
Which means that for a 4D trackball, some things that look like straight line gestures are actually going to be curved — in particular they will curve around the “front” of the 4D trackball.
Tomorrow we’ll see just how many such curves are needed for this.