Today I had a great brain-storming session with friends/colleagues Murphy Stein, Vi Hart and Charles Hendee (and briefly Jan Plass) about all sorts of things fun and mathematical. Among the many things we discussed, one that really resonated with me came out of this image, the original of which can be found in a wonderful discussion about Hyperbolic Geometry by Vladimir Bulatov.
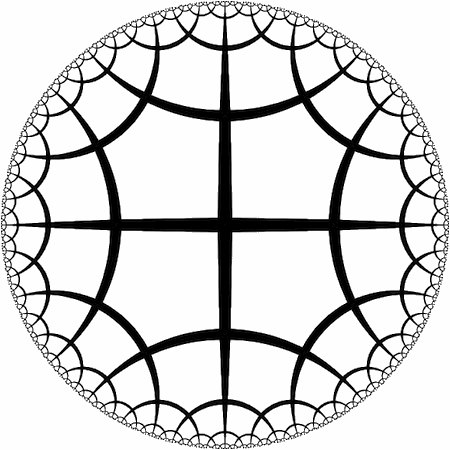
This is a basically a Poincaré disk model of the hyperbolic plane. That’s a way to look at the hyperbolic plane by cheating — distorting things to make them look smaller the further away they are from you. In the above picture the entire hyperbolic plane appears to fit inside the circle, but that’s just an illusion — things near the edge are really very very far away.
Unlike our boring old Euclidean plane, the angles of a polygon in the hyperbolic plane can vary, depending on the polygon’s size. And that makes the hyperbolic plane a lot of fun.
For example, in the picture above, the hyperbolic plane has been filled with regular pentagons of just the right size so that the edges at each vertex join at 90o. In the Euclidean plane you couldn’t do this — but the hyperbolic plane is way cooler than the Euclidean plane.
If you lived in a city based on the plan in the above picture, you could walk north, turn 90o right five times in a row, and end up where you started. Wherever you are standing, everything would look pretty normal, but objects that are far away would look weirdly distorted and too small — as though perspective itself were operating on overdrive.
When I look at this picture, I imagine a shared on-line world — maybe something like The Sims, but in a hyperbolic geography. People would live in pretty houses on nice streets, with manicured lawns, except that the city blocks would be shaped like pentagons, and five right angle turns will always get you back home.
How about the fact that with the same radius of a circle in Euclidean and in Hyperbolic the area of the second one will be immensely bigger?..
And also try googling hyperrogue.
Ha! So It took only five and a half years after my post for somebody to finally come out with this game. 🙂