“I tried to follow your design rules for drawing an octahedron,” Trey says when they meet again the next day. “It’s our nearest equivalent to your diamond.”
“That is very solid of you,” Ariel replies.
“I kept your idea,” he continues, “of using red for ‘near’ and blue for ‘far’, with orange and teal for ‘near-ish’ and ‘far-ish’.” Also the whole notion of using tapered lines for edges that slant away in the extra dimension.”
Ariel is very pleased that someone of such obvious depth is adapting her design ideas. “So what does this three dimensional diamond — this thing you call an ‘octahedron’ — look like?”
Trey places the picture into Ariel’s two dimensional plane:
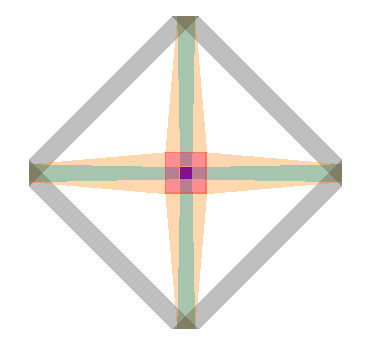
“Oh, I see,” Ariel says, after looking at the picture a while. “The grey edges are the parts that are actually in my world, with the orange/red sticking out in one direction into your third dimension and the teal/blue parts sticking out in the opposite direction.”
“Exactly!” Trey says, pleased at how quickly she is catching on. “And you can see how it’s really different from the cube I showed you yesterday.”
“Yes…” she replies, deep in thought. “The cube was really made of … let me see … six squares: Left, right, top, bottom, and those directions you call ‘front’ and ‘back’. But this octahedron thing has…” she frowns. “Hmm, it’s very weird.”
“Here’s a hint,” he says, “There’s a reason it’s called an octahedron.”
“Aha!” Ariel says, “Of course! There are eight triangles — four sticking out ‘nearer’ and another four sticking out ‘farther’. Wow, that is completely awesome. I wish I could visit your world sometime.”
“In a way,” Trey smiles, “you already have.”