If you recall, when you look head-on at a virtual trackball, you can’t actually see that your movements to “spin the ball up and down” and “spin the ball left and right” are creating curved motion. In the picture I first showed (below), the red and green arrows look straight to us, even though they are describing curves:
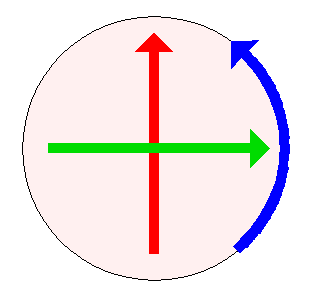
That’s because we were looking edge-on at the third direction. It’s like looking at a spinning bicycle wheel when the bicycle is heading toward you.
Similarly, if you are looking at a sphere floating in space in front of you, and you are looking edge-on into a fourth dimension, then your view of any spin that rotates the ball into that fourth dimension is going to have the same problem: You are basically looking head-on at a spinning bicycle wheel.
To turn a floating sphere into a four dimensional trackball, you just need to count how many ways there are to spin a bicycle wheel edge-on. It turns out there are three, since each of our familiar three dimensions can spin into that fourth dimension.
If you add the three ways of spinning a sphere that only involve our familiar three dimensions, you get six spin dimensions all together:
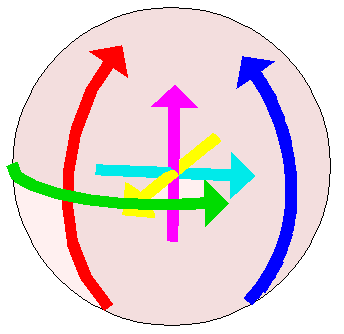
It should be pretty clear from the picture what’s going on: You can rotate the ball in three directions that don’t involve that fourth dimension at all, just like a regular track ball (the red, green and blue arrows).
Or, you can rotate it in a way that swaps any of our three dimensions for that fourth dimension (the cyan, magenta and yellow arrows).
Recall that some rotations on a regular virtual trackball require moving your finger in a straight line on your iPad screen (as in the first picture above). Something similar is happening here.
Namely, on a 4D virtual trackball you make those last three rotations (cyan, magenta and yellow) by moving your hand in a straight line inside the sphere that is floating in front of you.
I find it thrilling that you can manipulate a 4D object while staying safely inside our little 3D world. We’re working on building this stuff right now at NYU, using the Oculus Rift and our own hand tracking software. I will let you know when we have something cool to show.
This also means you can get gimbal lock in all sorts of new ways. Yippeeee!!!
There shouldn’t be any gimbal lock if you compute the rotation iteratively. Each iterative movement of your hand can be decomposed a radial component and a component around the sphere. The radial component can be used to compute iterative rotation in the xw,yw,zw subspace, and the component around the sphere can be used to compute iterative rotation in the xy,yz,zx subspace.
This is just an extension of what is already done with virtual trackballs for 3D rotation: Any small movement provides a direction and a length. Direction can be used to compute a perpendicular rotation axis, and length provides the rotation magnitude.
http://hop41.deviantart.com/art/4-Dimension-Sections-326951938
saw it, thunk of you.