Some years ago I was having a conversation at a conference with an artist. The topic got around to the classic computer game of Asteroids.
I was talking about how cool it was that when your ship goes off to the right of the screen, it always come back again from the left. And when it goes off the top of the screen, it comes back in on the bottom. So you never need to hit a wall.
“Basically,” I said, “the game is played on the surface of a torus.”
“No,” he said, “that means it’s on the surface of a sphere.”
I needed a way to convince him. So I came up with the following explanation. “Imagine,” I said, “that one person playing is traveling in an endless loop horizontally [the blue line in the image on the left], and another person is traveling in an endless loop vertically [the red line in the image on the left]. Those two people will meet in only one place.
“But if it were on a sphere, they would meet at two places: In both the front and the back of the sphere [like in the image in the middle]. But since they only meet in one place as they loop around, it’s just like a torus [like in the image on the right].”
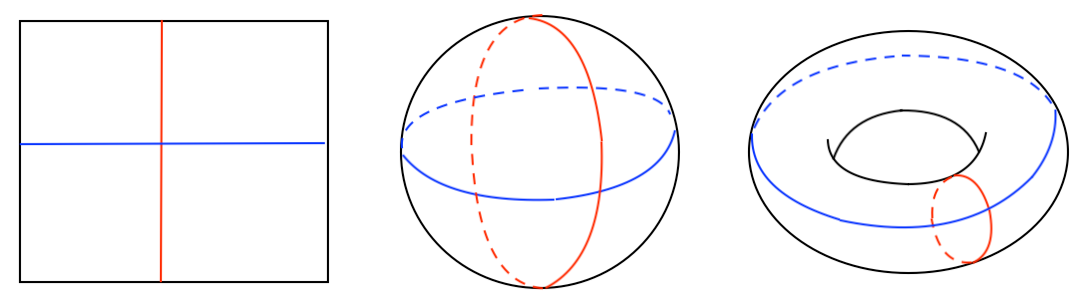
He thought about it for a moment, and then said “Yes, I see it now. You’re right, it’s on a torus.” Which made me very happy, because the entire conversation had been just words — no pictures necessary.
Later that day I relayed this conversation to Vi Hart, who was also at the conference. She just looked at me for a moment, and then said “You know, that’s the definition of a torus.”
That was good to know.
Hi Ken,
Check this out!
https://www.visgraf.impa.br/olhar3d/nave/asteroids/
(topological and geometrical 😉
-LV
Very cool. Thanks!