Playing with an icosahedron, and thinking of it as a kind of sphere broken down into simple pieces, got me wondering what would be the smallest piece you could break a sphere down into, so that all the pieces were exactly the same size and shape. That way, if you wanted to assemble a big dome or sphere, you could just carry portable little pieces around with you.
By having all the pieces be identical, you wouldn’t need to worry about numbering or ordering them in any way. Of course you could make a sphere or dome by inflating something, which would also be cool, but I’m thinking of how to make a rigid sphere.
The best solution I’ve come up with is 60 little identical pieces. If you inflate an icosahedron out to a sphere, then you can divide each of its twenty now-curved triangles into three equal pieces, like so:
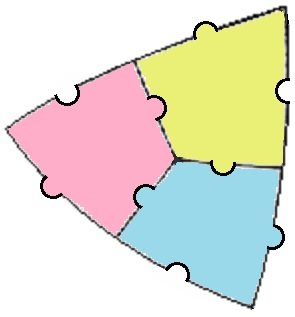
As you can see from the figure above, we can put little matching protrusions and notches into the edges of each piece, so that they will snap firmly together. Now we have a very compact way to “carry around” a rigid sphere as sixty identical little almost-flat pieces, and then assemble it together as needed. Of course if you only need a hemispherical dome (eg: as a portable planetarium) then you’d only need thirty pieces.
Unless somebody can think of a better solution.
Very interesting take on tesselation in 3d, but I think you need to clarify the acceptance criteria…
I can build a sphere out of squares, if the squares are small enough, and out of two hemispheres at the other extreme. What is the requirement? Fewer pieces, smaller pieces, or (I suspect) both?
Given the nature of the beast, I’m minded to suggest you apply a quality formula like q(n,s) = ns, where n is the number of pieces and s is their size.
Or perhaps the quest is to minimise the size of some bounding structure (a cuboid?) by volume?
Intrigued as usual.
The criterion is “the greatest number of identical pieces”. I don’t think a sphere can be built from squares.
There is infinite series of solutions with arbitrary large number of very thing
triangles: take spherical triangle with one vertex at the pole and two
other vertices at the equator. It is probably not what you are looking for.
The largest number of non-pathological identical pieces are 60 pieces,
you describe.
The boundaries of the pieces can be arbitrary curve starting and
ending at the symmetry points of icosahedron.
There are also 24 and 12 pieces configurations having rotational
symmetry of cube and tetrahedron.
Sorry, Vladimir. In my response to Phil I left out a word. What I meant was “the greatest number of identical non-degenerate pieces”. Although I do admire your creative use of the word “probably”. 🙂
Actually a criterion that is closer to the original intent of my post (note the word “portable” in the post’s title) is “a collection of identical pieces covering the sphere such that each piece has the smallest possible linear extent.” In other words, the set of pieces that is the most portable if you disassemble the sphere and carry around the pieces. Note that this immediately disqualifies the degenerate case.
Well, I love and hate mathematicians for ability to provide absolutely correct and absolutely useless answers.
Did you manage to build a dome like that? It would be nice to have an exact drawing of one piece, that would actually work out if produced and put together.
One problem is that even if you make an exact drawing, the target shapes are not flat. So a standard 2D printing technology doesn’t get you quite what you need.
It’s possible that you can cut the shape out of an appropriate flexible and stretchable material, which will “bulge out” appropriately when stressed by being fit together with the other 59 pieces of the sphere. I think one would need to experiment with various materials and thicknesses to see if there is one that works well.