Author: admin

What Vi pointed out to me the other day was that an apple slice is exactly the opposite of blowing a bubble in the following way: When you start to blow a bubble, say through one of those little plastic bubble blower rings, the ring itself doesn’t change size, but the soap film gets bigger (because of all that air pressure you’re adding on one side).

What happens of course is that the soap film bulges out, and starts to form part of a sphere. The harder you blow, the bigger part of a sphere you get. So you see, when you increase the area of a soap film, but not the size of its perimeter, it starts to go from flat to spherical.

But what is going on with a dried apple slice? Vi pointed out to me that the area of the apple slice starts to shrink as it loses water. But the perimeter of the apple slice doesn’t go down by as much. So it’s the opposite of a soap bubble — instead of a surface with too much area for its perimeter, we have a surface with too little area for its perimeter.

So if a too-much-area-for-its-perimeter shape is a section of a sphere, what is a too-little-area-for-its-perimeter shape?

Vi gave a wonderful answer to this last week at the annual Joint Mathematics Meeting, which you can see in this video.

I was going to continue talking about some cool math stuff, but I realize that today it is more important to speak out about an astounding act of bravery that we have all witnessed in the last week. I am referring, of course, to Sarah Palin’s speech in response to the tragic shootings in Tucson last weekend.

While our president has become distracted by irrelevant niceties such as honoring the dead, mourning the tragedy, calling for solidarity among Americans, and asking us all to rise to our better natures, Sarah Palin has been tackling the real evil here. Namely, the Blood Libel against the former governor of Alaska.

Let me say at the outset that there is absolutely no evidence that Ms. Palin has engaged in arcane Cabalistic rituals involving the innocent blood of murdered Christian children. There are no photographs, no tell-tale emails, no paper trail. Even Wiki-leaks has not found anything concrete to link Palin to the ritualistic slaughter of young Christian boys and girls.

Yet apparently the rumors are out there. Why else would a public figure of her stature use this occasion to deny Blood Libel, rather than talk about, say, the little nine year old girl who was shot to death because she was caught in the gunman’s crosshairs (oops, sorry Sarah, I know “crosshairs” is a sensitive word).

It take a person of immense courage and fortitude to stand up to the liberal media, to speak not about the federal judge who was tragically murdered by a madman, or the U.S. Congresswoman who lies in critical condition with a bullet through her brain, but rather to forcefully deny, once and for all, having used the blood of murdered children in one’s secret religious rituals.

After all, should history be any judge, then if people believe the Blood Libal against Palin, they will rise up and storm her village, massacrng her entire tribe down to every last man, woman and child. So Sarah is right to focus attention on the real danger that such a tragedy might occur, no matter how much the “mainstream media” annoyingly insists on talking about some dead nine year old brat who can claim credit for nothing more than having been at the wrong place at the wrong time in Tucson.

Sarah knows that all true Americans support her, because we know that she is the real victim here, and it’s important not to let the haters win.

Besides, the Blood Libel against Sarah Palin couldn’t possibly be true. After all, she’s not, um, you know, Jewish.

Yesterday I had a conversation with Vi Hart in which she made me see that drying an apple slice is exactly the opposite of blowing a bubble.

You probably think I’m speaking in hyperbole. Well, actually I am, but only on the surface. Tomorrow I will explain.

I had a fascinating discussion with a friend the other day about mood regulation. If we actually develop a reliable capacity to regulate our moods at all times, would life be better or worse? Ted Selker presented a wonderful speculative paper a few months back on the idea that perhaps 20 years in the future we might each have a constant feed drip that would automatically pump the optimal hormones and other chemicals into our blood stream as we go through our day, all under computer control. He didn’t weigh in on whether this was a good thing or a bad thing — he merely pointed out that it is going to be a possible thing.

Frankly, I think we’re going to have the technical capability to do this, on a widespread consumer level, in far less time than twenty years. And when we do, what kind of a world will it be? Will there be less violence, because peoples’ regulators will automatically calm them down before they get too worked up, sort of like a personal cruise-control?

Or might it go the other way? My friend was concerned that individuals fall get into dangerous positive feedback loops, in which an off-kilter mood adjustment might lead to bad judgement, which could cause a spiraling out of control. And so, will self-mood-regulation be seen as a privilege rather than a right (much like a driver’s license), and will your license to regulate your own mood be revoked if you abuse it?

Will the artistic impulse begin to wither away and die, as would-be artists find themselves perfectly content, with no angst to work out or express through their work? And if this happens, will anybody care? Will we gradually degenerate into a society of placid lotus eaters?

Or will we, after an initial period of adjustment, learn how to use these new capabilities constructively — to exercise more, eat better, do our work with greater enthusiasm and vigor, be kinder to our friends and family, get in touch with our sexuality, find more joy in life and in each other?

Of course in the worst case things could all go horribly wrong. And if they do, will we still have the capacity to care?

Today I played around with my little fractal program from yesterday, seeing what sorts of shapes I could make. The all-red color scheme was too limiting, so I made several new versions that add a splash of color.

Below you can see a few of the shapes I found. If you click on the image you can see the results in high resolution.

In 1904 the Swedish mathematician Helge von Koch published a paper about a wonderful fractal curve, which since then has variously been called the Koch Curve, Koch Star or Koch Snowflake. I talked about this curve recently on this blog, because I used it to create a Fractal Holiday Decoration on my 3D printer.

Today I wanted to create a way for you to make your own fractal shapes. In the last few days I’ve done a little research on the web around the idea of “making your own fractal”. What I’ve learned is that there are a lot of sites that want to sell you software to make your own fractals, and I was appalled to discover that they’re all pretty much the same.

What these sites all say, in essence, is: “You, the person reading is, are a complete idiot. But there are other people out there somewhere who are a lot smarter than you. They are called ‘mathematicians’, and they do this really arcane, magical mystical thing called ‘mathematics’ — something that you could never hope to understand. But just because you are a hopeless simpleton, well that doesn’t mean you shouldn’t have any fun, or even be allowed outside on occasion. So I’m going to do you a really big favor and let you send me ten bucks so I can give you a way to play around with the Mandelbrot set. You won’t have the faintest idea what’s going on (being a complete idiot and all), but you’ll still be able to make pretty pictures with nice colors.”

I don’t know about you, but there is something about this kind of sales pitch that I find vaguely insulting.

In fact there isn’t anything obscure or mysterious about fractals. Fractals are simply shapes that continue to repeat themselves at progressively smaller scales. If you understand that straightforward concept, then you’re a mathematician. My goal today was to create a sort of fractal playground, so you can make your own fractal shapes — with no mystery at all about what you are doing.

If you’ve read my post about making those holiday decorations, you’ll recall that they were Koch snowflakes, created with a very simple recipe:

1. Start with a triangle.
2. Glue a 1/3 scale version of the original shape onto the middle of each edge.
3. Repeat step (2) with the new smaller edges, until you either get bored or die of exhaustion.

 

Today I wrote a program to allow you to vary that recipe. Basically, you can create your own starter shape, and see what kind of fractal you get. You can vary how many levels to repeat (the more levels, the crinklier your fractal gets), and what kind of shape to start with (three sided, four sided, etc).

It’s really astonishing how many interesting shapes you can get this way. Try it for yourself by clicking on the image below. Drag the points around to create your own starter shapes, and watch how the very simple recipe above produces a delightful variety of fractals.

Oh, and you don’t need to send me ten bucks. Fractals should be free. 🙂

The title of my previous post — “exogeometry” — was a play on the term “exobiology”, or the study of life beyond the planet Earth. Exobiology is, necessarily, a somewhat speculative science, since we humans have not yet really found any life beyond the planet Earth. But, as they say, it never hurts to be prepared.

This evening I had the pleasure of listening to a number of Jazz ensembles, which were all participating in a little Jazz festival here in New York City. I was struck by the wide variety of music that fits under that category “Jazz”. And I found myself wondering, how much of our appreciation of music is determined by the fact that we are human? Nearly all of us are endowed with the natural wind instrument that is the human voice, as well as a sense of hearing attuned to that voice. And our ten biological fingers have, over the course of millenia, steered the development of musical instruments — from the piano to the trumpet — that are quite well suited to be played by human hands.

Even beyond these mere physicalities, my friend Gary Marcus has been studying how our brain has biologically evolved in ways that are well suited to the cultural evolution of what we call music. If you pick up an infant, it will start to kick its legs in a bipedal rhythm, long before it is capable of walking. That 1-2-1-2 rhythm — the most fundamental rhythm in all of our music — is embedded into the very fabric of our cerebellum.

But even beyond music, is our entire notion of aesthetics predicated on the accidents of nature that caused us to be evolved the way we have? This magnificent brain which is our common birthright, how completely does it define the limits and extent of what we call visual art, or drama, or humor?

And beyond even these questions, how much does our human brain influence our ultimate human art form — the purest of all our aesthetic arts — our study of mathematics? Is the beauty of the Pythagorean theorem a feature of the universe we inhabit, or is it actually a a consequence of the way our brains are wired to aesthetically experience that universe?

Would a sentient creature from another star system share our awe and delight at how elegantly Euclid established that the prime numbers go on without bound? Or Canter’s simple and lovely diagonal proof that the numbers between 0 and 1 are uncountably many?

Unlike aesthetic questions in music or the visual arts, our mathematical arts express forms of beauty that go beyond mere accidents of physical biology — or even the laws of physics. And yet, the state of exoaesthetics being what it is, we cannot yet know whether the appreciation of even such pure forms of beauty can exist beyond the human brain.

Today I thought it would be fun to create shapes by writing a program that computes and then draws one continuous line — sort of a mathematical Etch-a-Sketch or Spirograph. This is actually the oldest idea in computer graphics, since John Whitney pretty much started the field of computer animation over half a century ago by doing something like this.

My goal was to see whether some very simple rule could produce a large variety of beautiful shapes. I didn’t have any specific approach in mind, other than this general idea. I tried all kinds of different things this evening, and the result I liked best was a little program that lets you create a very large variety of shapes, including all of the shapes below, by moving your mouse around:

Looking at all these lovely forms, I feel as though I’ve stumbled across some mathematical Burgess Shale. Or maybe this is just a single fabulous creature who lives in some higher dimensional space. Perhaps it looks to us like different creatures because it keeps turning in various directions, as it swims around in its high dimensional world.

I suspect there are many more shapes to be found in my program. You can click on the image above to find them for yourself.

The recipe is very simple:

      x = y = θ = 0
      Repeat 8000 times: x²
            x += cos θ / 10 x²
            y += sin θ / 10 x²
            θ += ( (x²q)^p + (y²/q)^p ) / 20

When you move your mouse, you are varying p and q.

Continuing from yesterday, I’ve been playing around with ideas about how to make original games that are like chess, but not exactly chess.

Today I sketched out a little interface, just to get a feel for what it might be like to create such games. It’s not finished yet (for one thing, you can’t yet play the game that you design), but noodling around with what I have so far should give you a sense of it.

As you can see in the image below, on the right are the different options for how a piece can move. You can mix and match such things as whether a piece can move by just one square or by any number of squares, or can travel in one, two, four or eight directions, or whether those directions are even or odd directions.

On the left side of the image, you can see the different kinds of pieces. Eventually I should provide a way for a piece to look like a king, queen, bishop, knight, martian, or Godric of Gryffindor, but for now the way the way a piece looks reflects the way it moves — just like the diagram in yesterday’s post.

The first six pieces on the left column are initialized to move like a pawn, knight, bishop, rook, queen and king, respectively. The last two pieces are something else entirely: one can move just one square at a time left or right, and the other slides any number of squares forward or back.

But the interface lets you redefine any piece to move in some other way. Click on the image below to link to the applet, and start designing your own game!

Doug’s commented on my “Practicing chess” post, saying that he’d like to write a program to show where the “dangerous” moves are — the ones where your piece could be captured — started me thinking about the whole process of writing computer programs to implement games.

The thing about programming computers is that you always find yourself not just wanting to solve one problem, but rather to say “hmm, this is an interesting kind of problem. I wonder what general set of problems it falls into.” That’s also the thing about doing math, by the way.

So as I started thinking today about what Doug said, I found myself wondering “how could you make it possible for somebody to define the rules for a whole bunch of games — even their own original games?”

Thinking about it that way, I realized that defining the rules for chess isn’t all that complicated. There is “core chess”, which has almost ridiculously simple rules. And then there is “evolved chess” — those extra rules that got added over time to make the game more interesting. Evolved chess has added just the five following rules:

   — Pawns can move two spaces forward on their first move.
   — The en passant rule for pawns capturing pawns.
   — Pawns capture on the diagonal.
   — The “castling” move for a king and rook.
   — Promoting a pawn when it gets to the end of the board.

Except for the above few extra rules, chess has only the following few core rules for how its pieces move:

   –Which directions a piece can move.
   –Whether a piece moves (i) to the nearest space, or (ii) any distance.

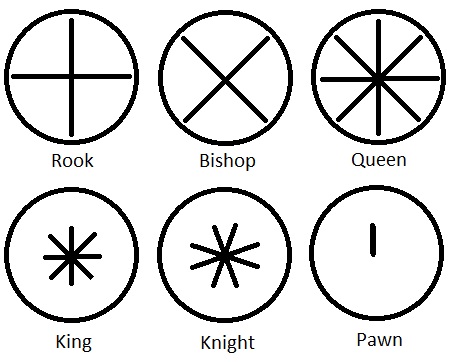
That’s because chess pieces always move in some regular pattern of compass directions around a circle. For example, a Rook or Bishop can move in only four directions, whereas a Knight or King or Queen can move in eight directions, and a Pawn can only move in one direction.

The complete set of rules for core chess can be expressed as a simple table:

Rook:     4, even, any      Bishop:     4, odd, any      Queen:     8, even, any      King:     8, even, nearest      Knight:     8, odd, nearest      Pawn:     1, even, nearest

What the above table says is that the Rook moves in any of four even compass directions (North, East, West, South), to any distance. The Bishop moves in any of four odd compass directions (NE, NW, SW, SE), to any distance. The Queen moves in any of eight even compass directions (N, NE, E, SE, S, SW, W, SW) to any distance.

Meanwhile, the King moves in any of eight even compass directions to the nearest square. The Knight moves in any of eight odd compass directions (NNE, ENE, ESE, SSE, SSW, WSW, WNW, NNW) to the nearest square. The Pawn moves in only one compass direction (North) to the nearest square.

So if you wanted to give somebody a way to create their own original board game, you could mostly just let them fill out their own version of the above table, one for each kind of piece they want to have.

If we did that, then who knows? Maybe some natural game-making genius out there will come up with an original game that’s incredibly cool.