Month: April 2013

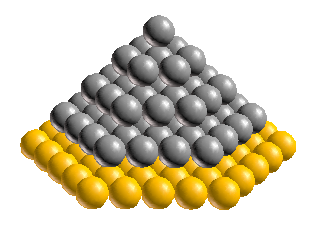
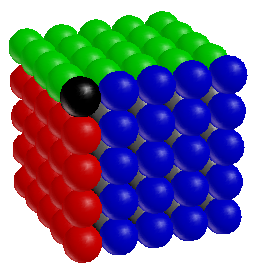
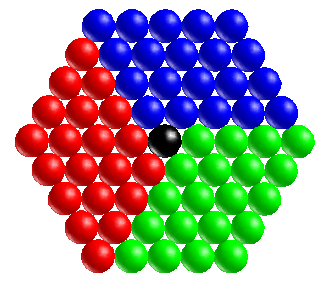
I would love to talk about the fourth dimension here, but I think for many people it would be a stretch. So maybe it’s a good idea to start with a different question: How would you explain our three dimensional world to a creature who lives in only two dimensions? How, for example, would you explain a cube, or a pyramid, or an octahedron?

Of course Edwin Abbott got here nearly 130 years ago. But he was limited by the relatively scarcity of computers in those days, so perhaps we can take the argument further.

Yet I wonder whether that is even the best place to start. Maybe we should begin by placing ourselves in the (very flat) shoes of those two dimensional creatures. Imagine them looking sadly upon beings who exist only in a one dimensional universe — that is, inside a line.

I imagine our two dimensional creatures would feel very grand indeed, compared to such poor monodimensional souls. “How,” they might well ask themselves, “can we explain something as complex as a square or a triangle to someone who can perceive only one dimension?”

The answer, of course, is to appeal to their one dimensional friend’s intelligence and imagination. But more on that tomorrow.

The sad events around Boston these last two days have been so overwhelming that the event I was going there for has been postponed. So I find myself with an extra day in New York.

It’s important to use that sort of extra time productively. For example, thinking about interesting ideas.

Ever since my blog post about the pyramid of spheres, I have found myself thinking about how beautifully those shapes fit together. And I remembered that when I was a kid, I was completely fascinated to discover that exactly six quarters can be fit around a quarter — to make a perfect hexagon. To me this was pure magic.

You can sort of do something like this in three dimensions, since twelve spheres can fit perfectly around a sphere (I once made an on-line visualization of this). But it’s not as pretty in three dimensions — the resulting arrangement doesn’t form a perfectly regular structure.

Yet it turns out that in four dimensions it all becomes perfect again. Just as in two dimensions you can fit six circles perfectly around a circle, which extends into a perfectly regular pattern that goes on forever, in four dimensions you can fit twenty four “hyperspheres” (spheres in four dimensions) perfectly around one hypersphere, which also extends into a perfectly regular pattern that goes on forever. The beautiful four dimensional shape that does this is called a “24-cell”.

I know 4D is a touchy subject for many people. After all, we can’t actually visit the fourth dimension. But hey, the magnificent thing about being human is that we can think about things that don’t physically exist. These things include the very words that come out of our mouths, as well as love, honor, joy, happiness, and a sense of humor.

In fact, just about all of the things we care about most deeply are things that don’t physically exist. So what’s wrong with thinking about the fourth dimension?

In 1995 I saw a wonderful and sadly overlooked film called “Things to do in Denver when You’re Dead”. Everyone in the cast, which included Christopher Walken, Andy Garcia, Gabrielle Anwar, Christopher Lloyd and Steve Buscemi, among others, was at or near their very best, and the writing by Seth Rosenberg was simply amazing.

The story was simple, and featured a powerful existential question: If you know you’re going to die in a matter of days, how do you spend your remaining time on earth? And for that matter, what does time even mean in such circumstances?

Anyone familiar with Tom Stoppard will immediately recognize that the title is a clever riff on his “Rosencranz and Gildenstern are Dead”, which ponders similar questions — which is itself in turn a clever riff on “Hamlet” (which tackles existential questions of its own).

A conversation today reminded me that this film was an influence on my thinking about interactive narrative. The conversation came in the wake Emily Short’s recent brilliant talk about interactive narrative at GDC. My take-away from Emily’s talk was that it might be more interesting let players manipulate not what interactive characters do, but rather how the characters do it.

In other words, you don’t get to decide your fate, but you do get to decide what you will do on your way to your fate.

And then I remembered that I had done some experiments along these lines when I was working with Athomas Goldberg on our “Improv” research project. Shortly after having seen “Things to Do in Denver When You’re Dead” I had put my little Improv characters into a chess game. They couldn’t affect the outcome of the game — which was played by real people. Rather, the characters would react emotively to the moves of the game.

Imagine for example, a pawn and a knight who have fallen in love. As one of them falls in the heat of battle, they say their tearful goodbyes. Now imagine a toolbox for creating such character personalities and for generating little scenarios between them. Characters can be comic, tragic, or simply absurd.

This direction opens up new possibilities for interactivity. Once we are freed from responsibility for plot, we can focus on character.

I called it, of course, “Things to do in Improv when you’re chess”.

I know that atrocities against humanity happen all the time around the world. Yet there is a difference between intellectual knowledge and emotional knowledge.

The horror of the bombing at the Boston Marathon hits me on an emotional level. These are my friends, my colleagues, my world. And so the sheer cruel insanity of such an act jars me deeply, while remaining beyond my understanding — I find it incomprehensible.

There might be a political element here, yet what sort of political agenda could be effectively advanced by the deliberate killing and maiming of children?

This coming Saturday I will be traveling up to Boston, where I will see many friends and colleagues. I’m sure the topic of the bombing will come up. Yet despite of the freshness of that horror, we will not let it define us.

This is the one victory we can always claim against the purveyors of death. Their actions inevitably lead to nothingness. Whereas even in the face of terrible sadness and loss, we will continue to find ways to celebrate each other — and this life, in all of its infinite joy and possibility.

This weekend past my friend and I
Through New York streets did roam,
And discovered tiny people.
Here’s the doorway to their home:

We knocked upon their little door,
Oh do not ask me why,
But we never got an answer
(I have heard they’re very shy).

When we return we hope to see
Their door is open wide,
Although I’m not quite certain
Just how we would fit inside.

Today Alex posted the following comment on this blog:

Thank you, but please allow me to ask one silly question. I think in many aspects of life, what scientist does is defining a problem, then finding out a solution. It seems like there is”solution” now. are there any problems we can solve with this fact, or it’s just a pure observation?

At first I was stumped. To me what is important about the relationship between the pyramid and the cube is that it is beautiful. It had never occurred to me that such beauty would require “defining a problem”.

And then I recalled something René Magritte once wrote, that his painting Le Modele Rouge (below) concerned “the problem of shoes”.

 
I do not know whether my joyous discussion about pyramids and cubes will end up solving any problems.

Meanwhile, it’s good to know that Magritte was thinking about the problem of shoes. Although I’m not entirely sure this makes him a scientist.

As requested by Alex, here is an old fashioned proof that packing spheres into a cube N on a side uses the same number of spheres as arranging them into an N-high hexagonal pyramid.

We already know that a 1³ cube uses just a single sphere — the same as a “pyramid” of height 1 — which is just a single sphere.

We just need to show that adding an Nth layer to a hexagonal pyramid uses the same number of spheres as incrementing from a cube of width N-1 to a cube of width N.

To get from an (N-1)³ cube to an N³ cube requires N³ – (N-1)³ more spheres. That’s N³ – (N³ – 3N² + 3N – 1) spheres, which simplifies to 3N(N-1)+1.

If we can show that a packed hexagon with N spheres on a side uses the same number of spheres, then we’re done. We do that as follows:

To go from our single sphere to a packed hexagon with 2 spheres on each side, we need to add 1 sphere for each of the hexagon’s six sides.

Similarly, to go from that to a packed hexagon with 3 spheres on each side, we need to add 2 spheres for each side of the hexagon.

So to build up to a packed hexagon with N spheres on a side, we need to add 1 + 2 + …. (N-1) spheres for each side of the hexagon.

The sum of the numbers from 1 through N-1 is N(N-1)/2 (here’s the proof on Wikipedia).

Putting it all together, we have six of those sums (because the hexagon has six sides), plus the one sphere in the center.

Which gives us 6×( N(N-1)/2 ) + 1, or 3N(N-1)+1.

As they say in latin class, QED. But I think the visual proof is a lot more elegant — and it didn’t require linking to the Wikipedia to explain picky details. 🙂

It’s amazing how much easier it is to make something clear in a visual proof — using pictures rather than equations. Just for comparison, I wrote down the proof I described yesterday using equations instead of pictures, thinking I would post that today.

I encountered two problems: (1) Most people who read this blog won’t be able to follow the equations. (2) Even if they did, there are too many steps.

The biggest difference is at the end, when I showed how those three faces of the cube (which I colored red, green and blue) magically flatten out into three parallelograms to form the hexagon (after you add that one sphere in the center).

From the picture, it’s immediately obvious how this works. But not from the equations. So a story that is simple and elegant when told in pictures becomes a lot less simple and elegant when told with equations.

I wonder whether there might be some sort of hybrid way of describing such things — something half way between equations and pictures, so that you can get the best of both.

The other day I mentioned how if you arrange spheres into a pyramid of hexagons, you get the same number of spheres as if you’d arranged them into a cube. Today I thought it might be nice to prove it.

Well, supposed we have just one sphere. We can think of this either as the tip of a pyramid or as a 1×1×1 cube. What we need to show is that every time we add a layer of hexagons to the base of the pyramid (to make a bigger pyramid), we get the same number of spheres as if we’d arranged the spheres into a cube.

So first, let’s ask how many more spheres there are in the N³ arrangement below right than in the (N-1)³ arrangement below left:

What we need to show is that this difference is the same as the number of extra spheres needed to add an Nth layer to a pyramid of hexagons. In the image below, the new layer is highlighted in gold:

Going back to the cubes, let’s color all of those extra spheres in the N³ cube:

Notice that we get three extra walls — each with N×(N-1) spheres — plus one extra sphere in the corner. But that’s exactly how many spheres we need to make a hexagon with N spheres on each side:

So there you have it. We just showed that each additional hexagon layer contains exactly the difference between an (N-1)³ cube and and an N³ cube. So now we can be sure that a pyramid of hexagons, stacked N high, will always add up to exactly N³ spheres!

The following Venn diagram seems simple enough. Two sets intersect to create a set that is smaller and more restricted:

Yet when it comes to people, this logic is often completely wrong. The place where Lennon and McCartney worked creatively together was far larger than the creative space each would ever claim on their own. The same goes for Gilbert and Sullivan, Abbot and Costello, Ashman and Mencken, Siegel and Schuster, Greenwich and Barry, Dannay and Lee, Rodgers and Hammerstein and many others.

And so we have what seems like a contradiction: When it comes to human creativity, the set of intersecting talent can be far larger than the set of talents possessed by either participant.