Because his work centers on statistics, my brother works a lot with probability. And the fundamental question of probability is: “Given several things that might happen, what are the odds that any particular one of them will happen?”
If two horses are racing (and if we don’t allow a tie), then we know for sure that one of those horses is going to win, and the other will lose. If the odds of the first horse winning are x, and the odds of the second horse winning are y, then:
x + y = 1
where 1 is certainty (or 100%, as people often call it).
To my brother, this situation could be pictured something like this:
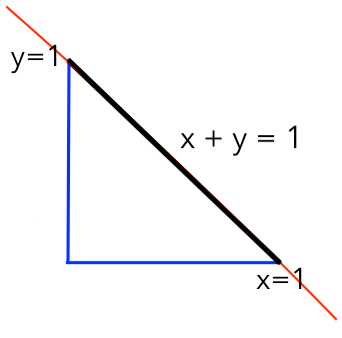
In the picture, x goes to the right, and y goes up. All of the possible outcomes of the horse race are along the diagonal black line that goes from bottom right to top left.
Further to the lower right (where x=1) it’s more likely that the first horse will win. Further to the upper left (where y=1) it’s more likely that the second horse will win.
That diagonal black line is exactly how my brother thinks of a regular simplex in one dimension — the shape that I drew as a horizontal line in yesterday’s post. For him, a one dimensional regular simplex isn’t just a line. It’s a long diagonal slice of a square.
The reason for this will become more clear when we go up one more dimension and talk about the three dimensional regular simplex — a triangle. Which we will do tomorrow.