The logic of this way of looking at a regular simplex starts to become clear when we consider the regular simplex in two dimensions: the equilateral triangle.
Suppose there are three horses in the race, and the odds of each horse winning are, respectively, x, y and z. Since it is certain that one of the three horses will win, we know that:
x + y + z = 1
But just like the race with two horses, we also know that the odds of any particular horse winning are at least zero. After all, there is no such thing as a negative probability. Well ok, sometimes there is, but not in horse races.
To my brother, the corresponding picture would look something like this:
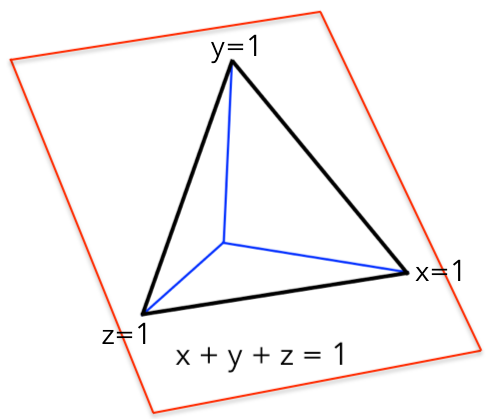
In this three dimensional diagram, the diagonal plane indicated in red shows all the places where x+y+z=1. The equilateral triangle outlined in black shows all of the places within this plane where x, y and z are all at least zero.
Which means that triangle shape represents all the possible sets of odds for our horse race. It is also, not by coincidence, the shape of the regular simplex in two dimensions.
We’re starting to see a pattern here. Does this pattern continue to work for higher dimensions? We will look at that question tomorrow.