Author: admin

In order to understand what’s going on with a 4D virtual trackball, let’s take a more careful look at a 3D virtual trackball.

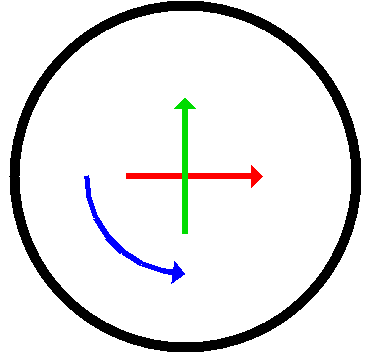
What you see is something like this:

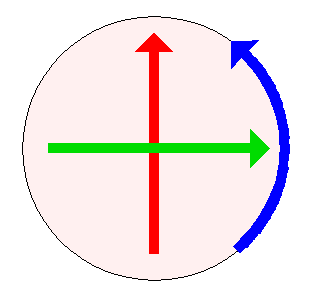
You can move your finger up and down (ie: in the direction of the red arrow), or from side to side (ie: in the direction of the green arrow), or around the circle (ie: in the direction of the blue arrow).

In each case, you are causing a sphere to rotate. This might seem mysterious to a denizen of Flatland, who does not have any direct perception of a third dimension. After all, the first two gestures look like straight line movement — very different from the circular movement of the third gesture.

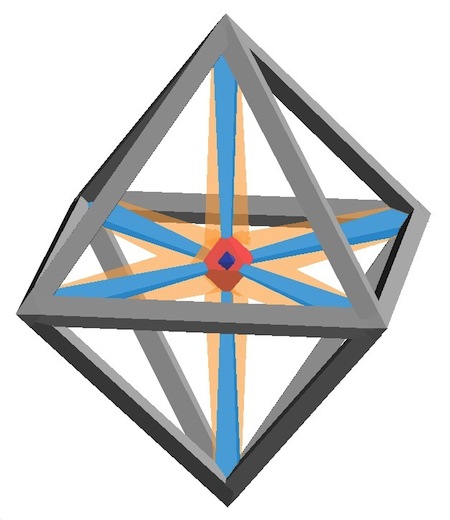
Fortunately we are, in fact, 3D creatures. Which means we can employ a great 3D power-up to see what’s going on: We can rotate our view of the object:

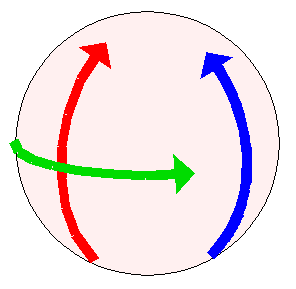
Now we can see, viewing from an oblique angle, that all three of the movements are actually circular arcs. The only reason the red and green gestures look straight is that the user cannot directly perceive the third dimension, since the z direction is perpendicular to our view. The red and green paths actually curve toward us, around the front of the sphere.

Which means that for a 4D trackball, some things that look like straight line gestures are actually going to be curved — in particular they will curve around the “front” of the 4D trackball.

Tomorrow we’ll see just how many such curves are needed for this.

It’s very cool that we can rotate things in three dimensions just by playing with a circular disk. After all, a disk is flat!

What’s also cool is that we can rotate things in four dimensions just by playing with a sphere. It’s not even that difficult to do — but it can be a little difficult to understand.

Just as you can rotate 3D objects by putting a finger down on a disk on a computer touch-screen, then moving the finger around inside the disk, there’s an equivalent action for a spherical region floating in space in front of you.

Namely, you can put your hand inside the sphere, pinch your fingers together to “grab” the sphere, then move your hand around inside the sphere (then unpinch your fingers to “ungrab”).

One way to think about this operation is that the volume inside the sphere is kind of like the area inside a circle, except in one higher dimension. As you move your pinched fingers around inside the sphere, you’re essentially rotating a 4D trackball.

But how do your movements inside that floating sphere translate to rotations in four dimensions? We’ll get to that tomorrow.

Continuing yesterday’s thought … if you were looking at a 4D object in front of you — holographically, the way Tera presented it to Trey — how would you rotate it, to see it from different points of view?

First let’s look at how people rotate 3D things on computers. One common way uses something called a “virtual trackball”. It’s basically just an image of a trackball, seen from above. When you drag your finger over the image, it does what a real trackball would do.

As you can see in the above image, a virtual trackball “rotates” around the vertical axis when you drag left and right (the red arrow), about the horizontal axis when you drag up and down (the green arrow), and about the axis that comes toward you when you spin around its edge (the blue arrow).

So here we have an example of a completely two dimensional thing that lets you rotate stuff in 3D. Perhaps we can do something similar for rotating stuff in 4D…

Sorry to switch the topic, but this evening I spent a delightful forty minutes with a friend, lost in conversation while walking through the rain in Paris.

If you’re going to walk through the rain anywhere, I highly recommend Paris. 🙂

Going back to the question of four dimensions… If you were a two dimensional being in Flatland, and you really wanted to understand 3D, you would want the most high quality visualization you could get of that mysterious higher dimensional world.

In that spirit, it seems to me that it would make sense to create the most vivid possible representation of our four dimensional object — even if it is impossible for such an object to exist in our world.

However we choose to simulate this four dimensional object, our simulation should appear before us with the same sense of “presence” as a real object. And if we reach out our hand, we should be able to touch it.

Sounds like a great opportunity to build a really good virtual reality experience.

Jumping out of our story for a little conversation…

I find this technique for visualizing higher dimensions — referred to as “Ariel’s design” in the story — to be very useful for my own understanding of 4D shapes. I am now much better able to, say, think about the parts of yesterday’s shape.

By the way, that shape is actually called a 16-cell, because it has sixteen three dimensional “sides”. It’s also sometimes called a hexadecachoron, which is just a fancy Greek way of saying “sixteen sided space”.

Using this approach, I can now understand the more complicated 24-cell much better than I could ten days ago (when I first wrote about it here).

Still, Trey’s question haunts me. To put the question simply: It is clear that a two dimensional square contains area. And it is clear that a three dimensional cube contains volume. But what sort of stuff does a four dimensional hypercube contain? What does it feel like to be ‘inside’ a hypercube? Is this something our poor human brains could ever get a feel for?

“Trey, I have something for you.”

Trey hears a voice, but he doesn’t see anybody. “Ah, Tera, how lovely to, um, hear you.”

“Thanks. I hope you still feel as positive when you see my picture of the four dimensional diamond shape.”

“Why, is there something wrong with it?”

“No, to me it looks like a perfectly lovely and symmetric shape. But your mileage may vary.”

Just then a shape materializes in the air front of him. But it’s not like any shape he’s ever seen before. “Are you sure that’s the four dimensional version of an octahedron?” Trey asks doubtfully.

“Well, yes, if we follow Ariel’s rules for how to draw these things. As you can see, I’m using little octagons for the corners.”

“I see a big octagon with some crosses inside it,” Trey says.

“Actually, nothing is inside. The big red corner is ‘near’ and the little dark blue corner is ‘far’. The edges that come ‘near’ to meet the red corner are orange, and the edges that go ‘far’ to meet the blue corner are teal.

“And what about all the stuff that’s gray?”

“Oh, those are the parts that lie inside your three dimensional space — neither near nor far.”

“So the fact that the red corner and the blue corner look like they’re in the same place…”

“…is an illusion,” she said, finishing his thought. “They look like they’re in the same place because our extra dimension is only seen edge-on in your world. Actually those two corners are as distant from each other as the distance from the bottom to the top of the whole shape.”

“Oh, I see now,” Trey says, “there are eight corners all together — the six in my world, plus near and far.”

“You’ve got it! And all eight corners are on the outside. How many edges do you see?”

Trey is starting to feel more confident. “Let me see … twelve grey edges, plus six orange edges, plus six teal edges … twenty four. Is that right?”

“Yes, that’s perfect! Any other questions?”

“Just one. A square or diamond has area inside. A cube or octahedron has volume inside. So what’s inside one of these?”

“Oh dear,” Tera says, “that’s a harder question.”

When Tera shows him what she has come up with, Trey is taken aback. “That’s amazing! It just appeared in the air, like a hologram.”

“No biggie — we just call that a picture. Those flat things that you call pictures are so lame.

“Well,” Trey says, “we also have sculpture.”

“True. I didn’t say you were hopeless. Anyway, what do you see?”

“I see two cubes, a fat red one and a skinny blue one, both in the same place. And I totally get that the red one is the one that’s ‘nearer’ in your fourth dimension. But shouldn’t the blue cube be smaller than the red cube, since it’s further away?”

“Ah,” Tera says, “that’s the clever thing about your friend Ariel’s design idea. She doesn’t make things bigger or smaller as they change in that extra dimension. She just makes the lines fatter or skinner — and of course she also uses color. If you make shapes bigger or smaller, which is what most people try to do, it can get a lot harder to see where everything is.”

“Oh, I see,” Trey says, “And the eight little grey cubes are the edges that go from ‘near’ to ‘far’, right? People in my world can only see them on-edge, which is why they look like little cubes.”

“Exactly!” Tera says. “I think you’re getting the hang of this.”

“OK then, what about something diamond shaped?”

“You mean something like your octahedron, but in four dimensions?”

“Yes please.”

“Hmm, I think I can have one ready for you by tomorrow.”

Trey thinks it’s a bit unfair that he can’t see his new acquaintance. “Where are you?” he asks.

“I’m just a little to the side of your three dimensional world. I could drop in — that is, part of me could — but that would sort of mess with the conservation of mass in your local vicinity, and the results might be unpleasant for all of us.”

“Well then,” Trey says, not wanting any trouble, “we shouldn’t go there.”

“Or more to the point,” Tera agrees, “I shouldn’t go there. I think you can hear me just fine from here — the air vibrations seem to do the right thing. And I can project 3D images into your world, so I don’t think we will have any problems communicating. Now tell me about this Ariel, and her wonderful design ideas.”

Trey is feeling very good about having introduced Ariel to the wonders of three dimensions. He is especially pleased to see her grasp this idea that things in his world can have shapes like squares and triangles around the outside. After all, Ariel couldn’t have any experience with a concept like ‘volume’ — something that people who live in a three dimensional world deal with every day.

So it must be strange for Ariel, he muses, to think of a square as being on the “outside” of some higher dimensional shape. “I wonder,” he ponders, “whether I, living here in a three dimensional world, could think of a cube as being on the ‘outside’ of some four dimensional shape.”

Just then he hears an unearthly voice. He can’t quite tell where it is coming from. The voice seems to be from everywhere and nowhere all at once.

He looks around wildly, trying to figure out who is talking to him. Just then an indistinct form appears — something that is right in front of him, and yet somehow not quite there at all. Perhaps, he thinks, trying to stay calm, there are worlds beyond this.

“Hello Trey,” the voice says, “my name is Tera. I hear you’ve been discussing some cool design ideas.”

“I tried to follow your design rules for drawing an octahedron,” Trey says when they meet again the next day. “It’s our nearest equivalent to your diamond.”

“That is very solid of you,” Ariel replies.

“I kept your idea,” he continues, “of using red for ‘near’ and blue for ‘far’, with orange and teal for ‘near-ish’ and ‘far-ish’.” Also the whole notion of using tapered lines for edges that slant away in the extra dimension.”

Ariel is very pleased that someone of such obvious depth is adapting her design ideas. “So what does this three dimensional diamond — this thing you call an ‘octahedron’ — look like?”

Trey places the picture into Ariel’s two dimensional plane:

“Oh, I see,” Ariel says, after looking at the picture a while. “The grey edges are the parts that are actually in my world, with the orange/red sticking out in one direction into your third dimension and the teal/blue parts sticking out in the opposite direction.”

“Exactly!” Trey says, pleased at how quickly she is catching on. “And you can see how it’s really different from the cube I showed you yesterday.”

“Yes…” she replies, deep in thought. “The cube was really made of … let me see … six squares: Left, right, top, bottom, and those directions you call ‘front’ and ‘back’. But this octahedron thing has…” she frowns. “Hmm, it’s very weird.”

“Here’s a hint,” he says, “There’s a reason it’s called an octahedron.”

“Aha!” Ariel says, “Of course! There are eight triangles — four sticking out ‘nearer’ and another four sticking out ‘farther’. Wow, that is completely awesome. I wish I could visit your world sometime.”

“In a way,” Trey smiles, “you already have.”